Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2025
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
4.
Despreciando las masas de las varillas horizontales y de las cuerdas y sabiendo que la abeja de la izquierda tiene una masa de $0,100 \mathrm{~kg}$. ¿Cuál debe ser la masa de cada una de las otras figuras para que el móvil permanezca "equilibrado"?
Respuesta
💡 Importante: Para entender esta resolución es clave que primero hayas visto las clases de estática de cuerpo extenso, donde resolvemos vamos ejercicios de este estilo en video. Mi consejo es que veas primero las clases y resoluciones que aparecen en esa sección y después vengas a estos ejercicios de la guía, para seguir practicando.
Reportar problema
Si, lo voy a seguir aclarando hasta el último ejercicio 😅
Teniendo en cuenta que conocemos la masa de la abeja de la izquierda, vamos a arrancar de abajo hacia arriba ➡️ Me centro primero en la varilla horizontal que está más abajo, para averiguar la masa de la abeja de la derecha
👉 Pedimos que la varilla de más abajo esté en equilibrio
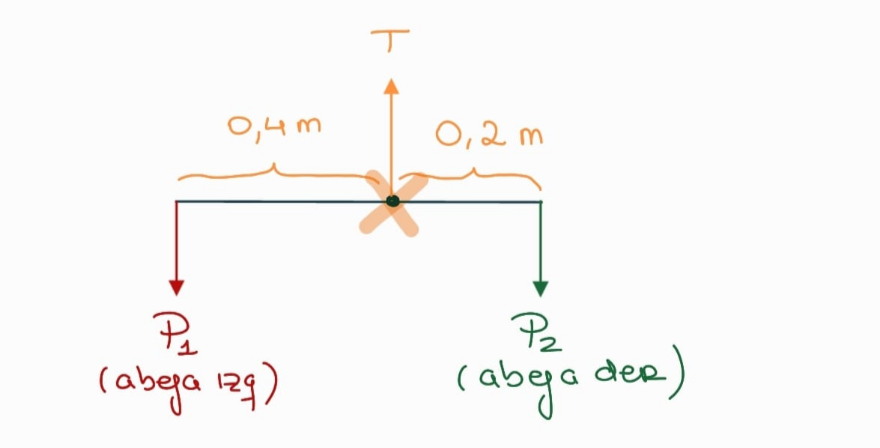
Elijo como centro de momentos el punto donde está aplicada la tensión de la cuerda (la que conecta esa varilla con todo lo de más arriba), eso es muy conveniente porque esa tensión no la conocemos ni tampoco nos interesa conocerla, así que eligiendo ese centro de momentos esa fuerza no va a estar generando momento. Calculamos el momento que genera el peso de cada abeja y pedimos que la suma de momentos sea cero:
Abeja de la izquierda 👉 $|M_{\text{izq}}| = 0.4 \text{ m} \cdot P_1 = 0.4 \text{ m} \cdot 0.1 \text{ kg} \cdot 9.8 \, \frac{m}{s^2} = 0.392 \text{ N} \cdot m$
Como esta fuerza me produce un giro en sentido antihorario, entonces le pongo signo positivo ➡️ $0.392 \text{ N} \cdot m$
Abeja de la derecha 👉 $|M_{\text{der}}| = 0.2 \text{ m} \cdot P_2$
Como esta fuerza me produce un giro en sentido horario, entonces le pongo signo negativo
Pedimos ahora que $\sum M_{(o)} = 0$ y despejamos $P_2$
$0.392 \text{ N} \cdot m - 0.2 \text{ m} \cdot P_2 = 0$
$P_2 = 1.96$
y como $P_2 = m \cdot g$
$m \cdot 9.8 \, \frac{m}{s^2} = 1.96$
$m = 0.2 \text{ kg}$
Por lo tanto, la masa de la abeja de la derecha es $0.2 \text{ kg}$
Ahora subimos para analizar qué pasa con la varilla del medio...
👉 Pedimos que la varilla del medio esté en equilibrio
La clave acá está en darte cuenta que, el extremo de la izquierda, va a estar soportando un peso equivalente al que genera la masa de la abeja de la izquierda + la abeja de la derecha, o sea... $(0.1 \text{ kg} + 0.2 \text{ kg}) \cdot 9.8 \, \frac{m}{s^2} = 2.94 \text{ N}$
Entonces, con un razonamiento idéntico al que hicimos recién, podemos averiguar el peso de la ¿gaviota? de la derecha:
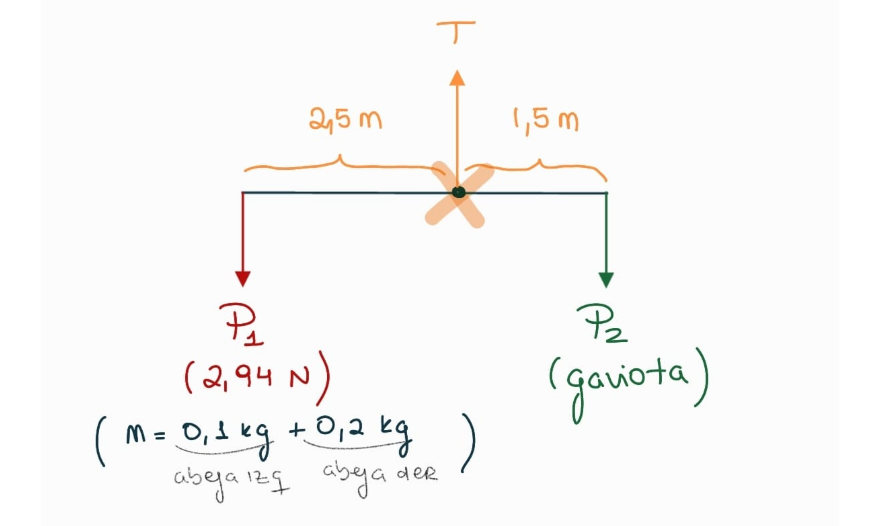
Peso de la izquierda (el de las abejas) 👉 $|M_{\text{izq}}| = 2.5 \text{ m} \cdot P_1 = 2.5 \text{ m} \cdot 2.94 \text{ N} = 7.35 \text{ N} \cdot m$
Como esta fuerza me produce un giro en sentido antihorario, entonces le pongo signo positivo ➡️ $7.35 \text{ N} \cdot m$
Gaviota de la derecha 👉 $|M_{\text{der}}| = 1.5 \text{ m} \cdot P_2$
Como esta fuerza me produce un giro en sentido horario, entonces le pongo signo negativo
Pedimos ahora que $\sum M_{(o)} = 0$ y despejamos $P_2$
$7.35 \text{ N} \cdot m - 1.5 \text{ m} \cdot P_2 = 0$
$P_2 = 4.9$
Y eso implica que la masa de la gaviota es $m = 0.5 \text{ kg}$
Nos faltaría ahora la varilla de arriba de todo...
👉 Pedimos que la varilla de arriba esté en equilibrio
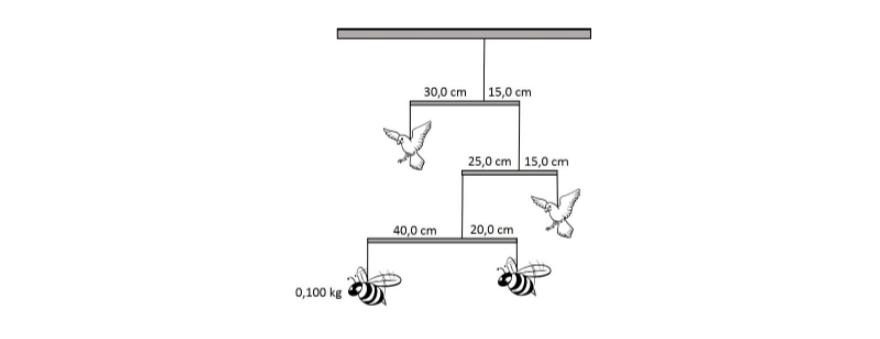
Se resuelve ooootra vez aplicando el mismo razonamiento que usamos para las primeras dos varillas -> Fijate que en este caso, el peso aplicado en el extremo de la derecha va a ser equivalente al de las masas de todo lo que quedó colgado de ese lado (las dos abejas y la gaviota) y el peso del extremo de la izquierda es una incógnita.
Usando la misma lógica y aplicando los mismos pasos que hicimos para las otras varillas, deberías estar llegando a que la masa de la gaviota de la izquierda es $m = 0.4 \text{ kg}$
Iniciá sesión o
Registrate para
dejar
tu
comentario.
🤖 ExaBoti
Esta conversación es privada
🤖 ExaBoti (privado)